Wavelet Tree
Authors: Benjamin Qi, Omri Jerbi
Wavelet trees support efficient queries for the kth minimum element in a range
Prerequisites
Wavelet Tree
Wavelet trees are data structures that support efficient queries for the k-th minimum element in a range by maintaining a segment tree over values instead of indices.
Focus Problem – try your best to solve this problem before continuing!
| Resources | ||||
|---|---|---|---|---|
| IOI | Introduces Wavelet Tree | |||
| CF | Link in blog post is broken, check my comment. | |||
Wavelet Tree Structure
To answer value-based queries efficiently, we'll create a segment tree where each node represents a range of values, instead of indices. Just like a normal segment tree, each subsequent level splits the range into two halves. Note that an index can appear in at most nodes.
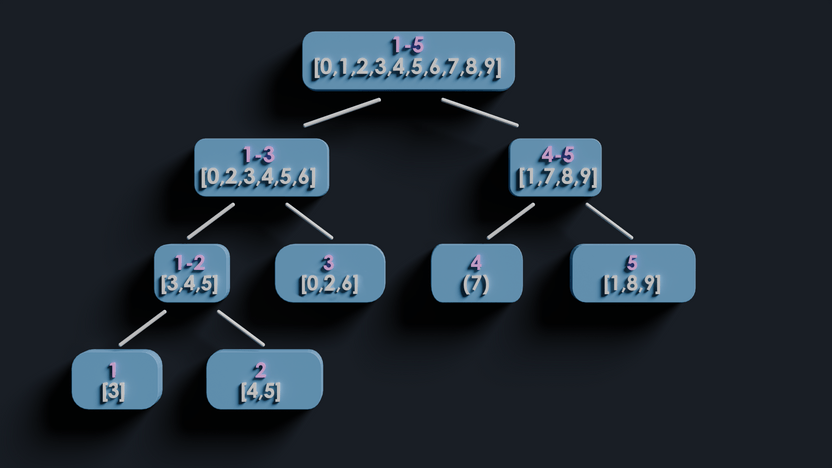
Wavelet Tree Visualization
Let's say our array is: Each node has an array representing the indices of every number between and
Solution - Range K-th Smallest
Before we solve this problem, let's consider a simpler version where we are asked, given a range, to count the number of occurrences of value .
Given a range , , count the number of occurrences of value x.
To calculate the number of occurrences from to , we can use the following formula:
This reduces the problem to counting the number of occurrences in a prefix.
One way to solve the problem is to go to the leaf node and perform a binary search for the number of indices less than However, let's explore a different approach that can also be extended to the second type of query.
Instead of binary searching on the leaf, we update as we recurse down the tree. If we can determine the position (index) of in the left and right children of a node, we can recurse down the tree and determine its position in the leaf node.
To find the position of in a node's left and right children, we need to determine how many indices are smaller than the middle value (mid) and precede . This can be done using a prefix sum.
Let's define:
- = as if [] is smaller than mid otherwise
- [] as prefix sum of
Formally
To update as we recurse down, we do the following:
- To know the value of if we recurse left, we use []
- If we recurse right, we use - []
Now let's try to solve our main problem.
Given a range , find the k-th smallest element
We will determine whether the answer for a given node is in the left or the right segment. We can calculate how many times the elements within the segments' ranges appear in our range using our first type of query. Note that this also works for non-leaf nodes using the following formula:
Similar
This is similar to counting how many times a value appears up to index in our previous query. We did this by using the new value at the leaf node. But now, we consider the difference between the updated and
Therefore, the occurrences of the left node are
Note that is the number of indices between and whose value is less than
- If is greater or equal to , it means the -th smallest element is in the left subtree. Therefore, we update our range and recurse into the left child
- If is less than , it means the -th smallest element is in the right subtree. We adjust k by subtracting from , update our range, and recurse into the right child
Notice
Notice we still update accordingly when we go left or right
The answer then will be the value of the node we end up on (leaf).
In conclusion we maintain our ranges l and r as we recurse down to our child, and when we reach the child node we can return - .
Implementation
Time Complexity:
C++
#include <bits/stdc++.h>using namespace std;constexpr int MAX_VAL = 1e9 + 2;struct Segment {Segment *left = nullptr, *right = nullptr;int l, r, mid;bool children = false;vector<pair<int, int>> indices; // index, value
Supporting updates
Let's support updates that change the value at index to .
We can traverse down to the leaf to remove the old element and also traverse down to add the new element.
Let's first solve for adding a new element; erasing is similar but the opposite.
So what do the updates change?
- Our indices vector
- Our prefix vector
At each step of our recursion, the indices vector will need to be modified; we need to insert the new index. Since we can no longer maintain a sorted vector of the indices, we will switch to a set.
On the other hand, to change the prefix vector, since each update could change our prefix vector a lot, we can't maintain just the normal vector. What we could do is use a sparse segment tree.
- erasing and inserting can be done by just setting the value to or at the specific index
- querying for a prefix can be done by querying the segment tree from to
This approach is not memory efficient and requires a segment tree's implementation. A more friendly approach would be using an order statistics tree, which is a binary search tree implementation in C++ that allows efficient queries for the rank of elements in a set. Querying for a prefix would then be equivalent to ().
Implemention
Time Complexity:
C++
#include <bits/stdc++.h>using namespace std;#include <ext/pb_ds/assoc_container.hpp>using namespace __gnu_pbds;template <class T>using Tree =tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
Problems
| Status | Source | Problem Name | Difficulty | Tags | |
|---|---|---|---|---|---|
| CF | Normal | Show TagsWavelet | |||
| SPOJ | Normal | Show TagsWavelet | |||
| COCI | Normal | Show TagsWavelet, Persistent Segtree | |||
| Kattis | Very Hard | Show TagsWavelet | |||
| GlobeX Cup | Very Hard | Show TagsWavelet |
Module Progress:
Join the USACO Forum!
Stuck on a problem, or don't understand a module? Join the USACO Forum and get help from other competitive programmers!